我室在二维材料晶格动力学研究方面取得系列成果
二维材料由于其优异的电学、光学、力学等性质,使得它们在电子器件、自旋器件、光学传感器、发光材料等领域有较广阔的应用前景。对于二维材料的实验表征、性能调控、器件应用,声子谱、热膨胀、以及力学性能的热效应等晶格动力学性质都是需要重点利用/考虑的。如果能够对二维材料晶格动力学原理建立起一个系统、普适、简洁的物理图像,那对未来的实验和理论研究,都会有较大的促进作用。
在最近的几年里,曾雉研究员小组广泛地研究了几类有代表性的二维材料(石墨烯相关材料、硅烯和锗烯相关材料、过渡金属硫族化合物)。利用第一性原理,模 拟了这些二维材料的电子结构、声子谱、格林埃森常数、热膨胀、以及力学性能的热效应,系统、深入、简洁地总结了二维材料晶格动力学的三个重要机理:1、质量效应;2、结构效应(包括低维效应和厚度效应);3、化学键强度效应。主要结论如下:
1、质量效应
原子质量对声子谱影响较大(同位素效应),对材料比热、自由能等影响也较大。但是,对二维体系的非简谐性质(比如,热膨胀和力学性能的热效应)影响较小,往往可以忽略。
2、结构效应
(a) 低维效应:
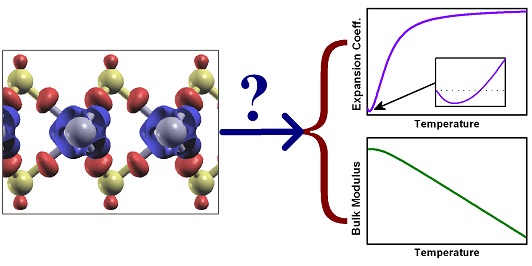
二维材料里面,会有类似连续薄膜波动的振动模式,叫做弯曲模式 (flexural/bending mode)。 常规声子模式在长波长下的色散关系是线性的(即,声速是常数),但是长波长的弯曲模式的色散关系是抛物线关系,这是一种低维效应。这种弯曲模式的存在,是 导致二维材料上的结构涟漪、负的格林埃森常数、和负的热膨胀系数的根本原因,其实也是一些三维材料(比如,硅、锗等半导体)里出现负的热膨胀系数的原因。 这通常也叫做薄膜效应或吉它弦效应。负的热膨胀会导致材料力学性能出现热硬化现象,但在高温下会因为声子的大量激发而出现常规的热软化现象。
(b) 厚度效应:
厚 度的增加有两种方式,一是通过不同层之间的堆叠(比如,多层石墨烯),二是通过增加单层内部的厚度(比如从石墨烯到功能化的石墨烯)。前者使得弯曲模式的 回复力和层之间原子键方向一致,后者使得层内部出现和垂直方向不正交的原子键,效果都是使得弯曲模式不再完全像连续薄膜里面的那些弯曲模式了。所以,厚度 无论通过哪种方式增加,二维材料里的弯曲模式都会损失一些二维特性,其格林埃森常数和热膨胀系数都会更加接近三维材料。有个常识就是:厚度越大,材料热力 学性能越靠近三维材料,而我们的工作很好地揭示了这个常识背后的根本机理。不过即使未来其它材料上出现反常现象,我们的机理还是可以用来揭示背后的反常机 理。
3、化学键强度效应
二 维材料多数是共价化合物,其原子键的强度通常由共价性和离子性之间的竞争来决定。在任何一个材料的一个声子模式里,一般都包含了一些原子键的局部拉伸和弯 曲。弯曲振动对格林埃森常数和热膨胀会有负的作用,机理和上述的薄膜效应是一样的,而拉伸振动是起正的作用。当原子键强度不够高的时候,拉伸振动的正效果 有时候会被弯曲振动的负效果给超过,反之亦反。这个机理不限于二维材料,块体Si, Ge, GaN等材料的LA模式出现较大负的格林埃森常数,及其低温下负的热膨胀系数,皆因为原子键强度较弱导致,而金刚石、石墨、单层石墨烯里的LA只有正的格林埃森常数,因为这些材料里面的碳—碳 键是超强的。对比不同过渡金属硫族化合物的格林埃森常数,原子键强度的机理会非常明显。除了通过影响格林埃森常数来影响热膨胀系数的正负和大小之外,原子 键强度还会通过弹性常数来影响热膨胀系数的数值大小。弹性常数小的材料有容易膨胀的趋势,即软的东西更容易被任何扰动改变尺寸(常识)。总的来说,原子键 强度通过格林埃森常数和热膨胀系数产生关联是一种非简谐效应(anharmonic effect),不仅决定大小,也决定正负;而通过弹性常数和热膨胀系数产生关联却是一种简谐效应(harmonic effect),只影响数值大小。
发表文章
[1] L. F. Huang and Z. Zeng, “Lattice dynamics and disorder-induced contraction in functionalized graphene”, J. Appl. Phys. 113, 083524 (2013).
[2] L. F. Huang, T. F. Cao, P. L. Gong, and Z. Zeng, “Isotope effects on the vibrational, Invar, and Elinvar properties of pristine and hydrogenated graphene”, Solid State Communications 190, 5-9 (2014). (属于上一个工作的附加故事)
[3] L. F. Huang, P. L. Gong, and Z. Zeng, “Correlation between structure, phonon spectra, thermal expansion, and thermomechanics of single-layer MoS2”, Phys. Rev. B 90, 045409 (2014).
[4] L. F. Huang, P. L. Gong, and Z. Zeng, “Phonon properties, thermal expansion, and thermomechanics of silicene and germanene”, Phys. Rev. B 91, 205433 (2015); arXiv:1503.03027 (2015).
[5] L. F. Huang and Z. Zeng, “Roles of mass, structure, and bond strength in the phonon properties and lattice anharmonicity of single-layer Mo and W dichalcogenides”, J. Phys. Chem. C 119, 18779-18789 (2015).


